Ferroelectrics

History

The phenomenon of ferroelectricity was discovered in 1921 by J. Valasek^[1] who was investigating the dielectric properties of Rochelle salt (NaKC₄H₄O₆.4H₂O). Barium titanate (BaTiO₃) was discovered to be ferroelectric in 1944 by A von Hippel^[2,3] and is perhaps the most commonly though of material when one thinks of ferroelectricity. While there are some 250+ materials that exhibit ferroelectric properties, some of the more common/significant materials include:


• Lead titanate, PbTiO3
• Lead zirconate titanate (PZT)
• Lead lanthanum zirconate titanate (PLZT)

Figure.1. The perovskite structure ABO₃, shown here for PbTiO₃ which has a cubic structure in the paraelectric phase and tetragonal structure in the ferroelectric phase.

Crystal symmetry and physical properties

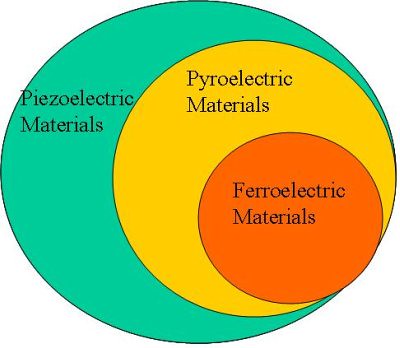
Twenty of the 32 crystal classes are so-called piezoelectric, and crystals belonging to one of these classes (point groups) display piezoelectricity. All 21 piezoelectric classes lack a center of symmetry (Note that Cubic 432 has higher symmetry). Any material develops a dielectric polarization when an electric field is applied, but a substance which has such a natural charge separation even in the absence of a field is called a polar material. Whether or not a material is polar is determined solely by its crystal structure. Only 10 of the 32 point groups are polar. All polar crystals are pyroelectric, so the 10 polar crystal classes are sometimes referred to as the pyroelectric classes^[III].

Figure.2. The relationship between the piezoelectric, pyroelectric and ferroelectric materials

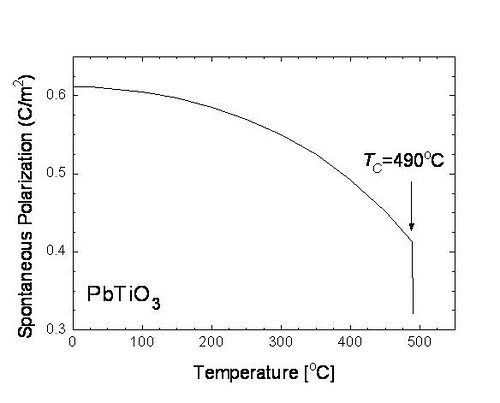
Below the Curie temperature, there is a dipole moment created in the structure. Therefore, a spontaneous polarization is found. One of the characteristics of ferroelectric materials is the initially rapid rise of their spontaneous polarization as their temperature drops below the critical value (Curie temperature), T_c. In crystalline ferroelectrics, this initial rapid rise in spontaneous polarization is due to the elementary dipoles in the material interacting with each other, producing an internal field which lines up the dipoles, eventually yielding saturation of the spontaneous polarization.

Figure.3. The spontaneous polarization vs. temperature plot of the PbTiO₃

Ferroelectricity

We have often commented that ionic susceptibility is not sensitive to variations in temperature. Although this is true for most substance, there is a class of materials which exhibits a marked departure from this rule: the ferroelectric materials. In these substances, the static dielectric dielectric constant changes with temperature according to the relation:

(1)

\begin{align} \epsilon_{r}=B+\frac{C}{T-T_{c}} , (T>T_{c}) \end{align}

where B and C are constants independent of temperature. This relation is known as the Curie-Weiss law, and the parameters C and T_C are called the Curie constant and Curie temperature, respectively.

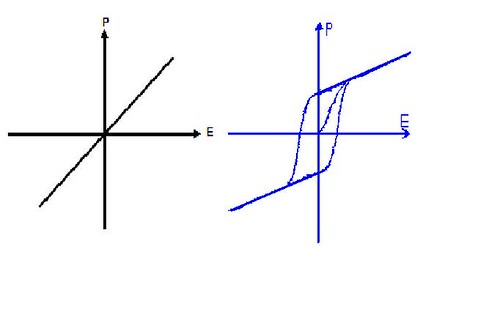
A phase transition occurs at the temperature T_C. Above the transition temperature, the substance is in the paraelectric phase, in which the elementary dipoles of the various unit cells in the crystal are oriented randomly. And below the transition temperature, the substance is in the ferroelectric phase ^[4].

Figure.4. (P-E) hysteresis loops of paraelectric phase (left) and ferroelectric phase

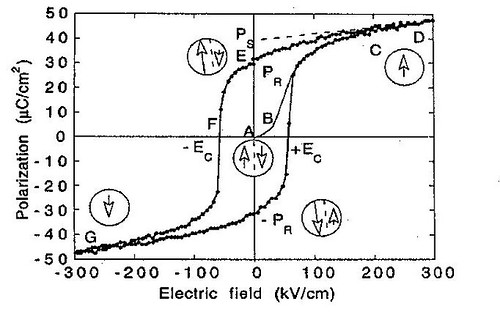
Ferroelectricity is a spontaneous electric polarization of a material that can be reversed by the application of an external electric field. Ferroelectricity is the phenomenon, by virtue of which some materials exhibit spontaneous electric polarization, even in the absence of any externally applied field. Ferroelectric crystals possess regions with uniform polarization called ferroelectric domains. Within a domain, all the electric dipoles are aligned in the same direction. There may be many domains in a crystal separated by interfaces called domain walls. A ferroelectric single crystal, when grown, has multiple ferroelectric domains. A single domain can be obtained by domain wall motion made possible by the application of an appropriate electric field. A very strong field could lead to the reversal of the polarization in the domain, known as domain switching. The polarization reversal can be observed by measuring the ferroelectric hysteresis as shown in Figure.5.

Figure.5. The ferroelectric (P-E) hysteresis loop. Circles with arrows represent the polarization state of the material at the indicated fields. The actual loop is measured on a (111)-oriented 1.3 μm thick sol-gel Pb(Zr_0.45Ti_0.55)O₃ film.

Polarization mechanism in ferroelectric materials:
Sources of polarizability^[IV]

Let us examine more closely the physical process which gives rise to polarizability. Basically, polarizability is a consequence of the fact that the molecules, which are the building blocks of all substances, are composed of both positive charges (nuclei) and negative charges (electrons). When a field acts on a molecule, the positive charges are displayed in a direction opposite to that of the field. The effect is therefore to pull the opposite charges apart, i.e., to polarize the molecule ^[5].

There are different types of polarization processes, depending on the structure of the molecules which constitute the solid (for details please see the Yuan's webpage ^[VI]). Basically, there are three types polarization mechanisms contribute to the total polarizability. In general, therefore, we may write for the total polarizability:

(2)

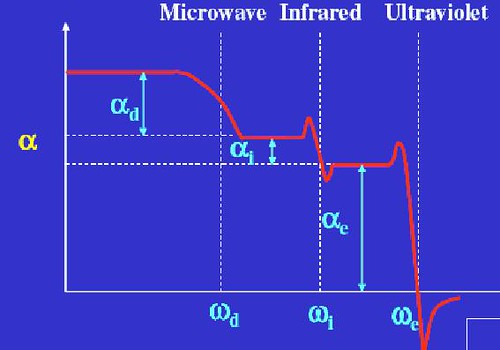
\begin{align} \alpha=\alpha_{e}+\alpha_{i}+\alpha_{d} \end{align}

which is the sum of the various contributions; $\alpha_{e}$, $\alpha_{i}$, and $\alpha_{d}$ are the electronic, ionic, and dipolar polarizabilities, respectively. The electronic contribution is present in any type of substances, but the presence of the other two terms depends on the material under consideration. Thus the term $\alpha_{i}$ is present in ionic covalent crystals such as Si and Ge, which are nonionic and nondipolar, the polarizability is entirely electronic in nature.

The relative magnitudes of the various contributions in (eq.2) are such that in nondipolar, ionic substances the electronic part is often of the same order as the ionic. In dipolar substances, however, the greatest contribution comes from the dipolar part.
The various polarizabilities may be segregated from each other because each contribution has its own characteristic features which distinguish it from the others. Dipolar polarizability, for instance, exhibits strong dependence on temperature, while the other two contributions are essentially temperature independent ^[5].

Figure.6. Total polarizability $\alpha$ versus frequency ω for a dipolar substance.

Landau theory of ferroelectric phase transformations ^[II,V]

Based on Ginzburg–Landau theory, the free energy of a ferroelectric material, in the absence of an electric field and applied stress may be written as a Taylor expansion in terms of the order parameter, P. If a sixth order expansion is used (i.e. 8th order and higher terms truncated), the free energy is given by:

$\Delta G=\frac{1}{2}\alpha_{0}(T-T_{0})(P_{x}^{2}+P_{y}^{2}+P_{z}^{2})+\frac{1}{4}\alpha_{11}(P_{x}^{4}+P_{y}^{4}+P_{z}^{4})+\frac{1}{2}\alpha_{12}(P_{x}^{2}P_{y}^{2}+P_{y}^{2}P_{z}^{2}+P_{z}^{2}P_{x}^{2})+\frac{1}{6}\alpha_{111}(P_{x}^{6}+P_{y}^{6}+P_{z}^{6})+\frac{1}{2}\alpha_{112}(P_{x}^{4}(P_{y}^{2}+P_{z}^{2})+P_{y}^{4}(P_{x}^{2}+P_{z}^{2})+P_{z}^{4}(P_{x}^{2}+P_{y}^{2}))+\frac{1}{2}\alpha_{123}P_{x}^{2}P_{y}^{2}P_{z}^{2}$

where P_x, P_y, and P_z are the components of the polarization vector in the x, y, and z directions respectively, and the coefficients, and the coefficients, $\alpha_{i}$, $\alpha_{ij}$, $\alpha_{ijk}$ must be consistent with the crystal symmetry. To investigate domain formation and other phenomena in ferroelectrics, these equations are often used in the context of a phase field model. Typically, this involves adding a gradient term, an electrostatic term and an elastic term to the free energy. The equations are then discretized onto a grid using the finite difference method and solved subject to the constraints of Gauss's law and Linear elasticity ^[II].

In all known ferroelectrics, $\alpha_{0}$ > 0 and $\alpha_{111}$ > 0. These coefficients may be obtained experimentally or from ab-initio simulations. For ferroelectrics with a first order phase transition, $\alpha_{11}$ < 0 and $\alpha_{11}$ > 0 for a second order phase transition.

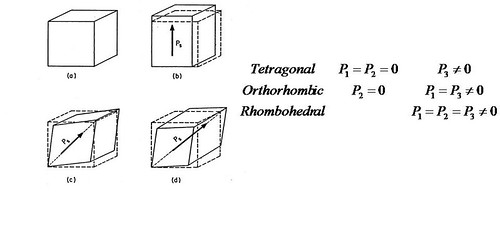
Figure.7. The relationship between crystal structure and polarization.

The spontaneous polarization, P_s of a ferroelectric for a cubic to tetragonal phase transition may be obtained by considering the 1D expression of the free energy which is:

(3)

\begin{align} \Delta G=\frac{1}{2}\alpha_{0}(T-T_{0})P_{x}^{2}+\frac{1}{4}\alpha_{11}P_{x}^{4} +\frac{1}{6}\alpha_{111}P_{x}^{6} \end{align}

This free energy has the shape of a double well potential with two free energy minima at $P=\pm P_{s}$, where P_s is the spontaneous polarization. At these two minima, the derivative of the free energy is zero, i.e.:

(4)

\begin{align} \frac{\partial\Delta G}{\partial P_{s}}=\alpha_{0}(T-T_{0})P_{x}+\alpha_{11}P_{x}^{3} +\alpha_{111}P_{x}^{5} \end{align}

(5)

\begin{align} P_{x}[\alpha_{0}(T-T_{0})+\alpha_{11}P_{x}^{2}+\alpha_{111}P_{x}^{4}]=0 \end{align}

Since P_x = 0 corresponds to a free energy maxima in the ferroelectric phase, the spontaneous polarization, P_s, is obtained from the solution of the equation:

(6)

\begin{align} \alpha_{0}(T-T_{0})+\alpha_{11}P_{x}^{2}+\alpha_{111}P_{x}^{4} \end{align}

which is:

(7)

\begin{align} P_{s}^{2}=\frac{1}{2\alpha_{111}}[-\alpha_{11}\pm \sqrt{\alpha_{11}^{2}-4\alpha_{0}\alpha_{111}(T-T_{0})}] \end{align}

and elimination of solutions yielding a negative square root (for either the first or second order phase transitions) gives:

(8)

\begin{align} P_{s}=\sqrt{\frac{1}{2\alpha_{111}}[-\alpha_{11}\pm \sqrt{\alpha_{11}^{2}-4\alpha_{0}\alpha_{111}(T-T_{0})}]} \end{align}

If $\alpha_{111}$ = 0, using the same approach as above, the spontaneous polarization may be obtained as:

(9)

\begin{align} P_{s}=\sqrt{-\frac{\alpha_{0}(T-T_{0})}{\alpha_{11}}} \end{align}

Applications for Ferroelectric Materials

The biggest use of ferroelectric ceramics have been in the areas such as dielectric ceramics for capacitor applications, ferroelectric thin films for non volatile memories, piezoelectric materials for medical ultrasound imaging and actuators, and electro-optic materials for data storage and displays [VII].
*Capacitors
*Non-volatile memory
*Piezoelectrics for ultrasound imaging and actuators
*Electro-optic materials for data storage applications
*Thermistors
*Switches known as transchargers or transpolarizers
*Oscillators and filters
*Light deflectors, modulators and displays

Reference

1. J. Valasek (1920). "Piezoelectric and allied phenomena in Rochelle salt". Physical Review
15: 537. and J. Valasek (1921). Physical Review 17: 475
2. A. von Hippel and coworkers, NDRC Reports 14-300 (1944), 14-540 (1945); A. von Hippel,
R. G. Breckenridge, F. G. Chesley, and L. Tisza, J. Ind. Eng. Chem. 38, 1097 (1946).
3. B. Matthias * and A. von Hippel Phys. Rev. 73, 1378 - 1384 (1948)
4. M. Ali Omar. "Elementary Solid State Physics"p.408. (ISBN 0- 201-60733-6)
5. M. Ali Omar. "Elementary Solid State Physics"p.381. (ISBN 0- 201-60733-6)

Reference websites
I. http://www.azom.com/details.asp?ArticleID=3593
II. http://en.wikipedia.org/wiki/Ferroelectric
III. http://en.wikipedia.org/wiki/Crystal_lattice
IV. http://mysite.du.edu/~jcalvert/phys/polariza.htm
V. http://en.wikipedia.org/wiki/Ginzburg%E2%80%93Landau_theory
VI. http://electrons.wikidot.com/polarization-of-ceramic-materials
VII. http://4engr.com/dictionary/catalog/1322/index.html